「迷子になったら動くな」を検証してみた
今日友達とホームセンターに行ったら迷子になってしまった。
いや、はぐれちゃっただけなんだけど、僕は携帯を持ってなかったし、この年で迷子センターに行くのもなーってことでしばらくウロウロして探した。
そこでふと幼い頃「迷子になったらそこから動くな、探される方がウロウロしてしまうと見つけにくくなるから」とママンに言われたのを思い出したんだけど、これって本当だろうかと思って検証してみた。
コードはgistにある。
動作させるとこんな感じ。
迷子になったホームセンターを模したマップを作って、それに対して人を2人だけ用意してランダムに配置し、見つけられるまでに行動した回数をカウントする。
「双方動いた場合」っていうのと「ママンだけが動いた場合」っていう2つの状況を100,000回ずつ試して、その行動回数の分布を見てみる。
このシミュレーションでは、ひとはステップごとに移動と向きを変えることができて、向いている方向に対象の人がいたら見つけたことになる。
結果はこんな感じ。 横軸が試行回数、縦軸がその試行回数で発見できた回数。 試行回数の最高値は16,811なんだけど、双方動いた場合の最高値は1,995なのでこのグラフは全体の一部だけの表示。
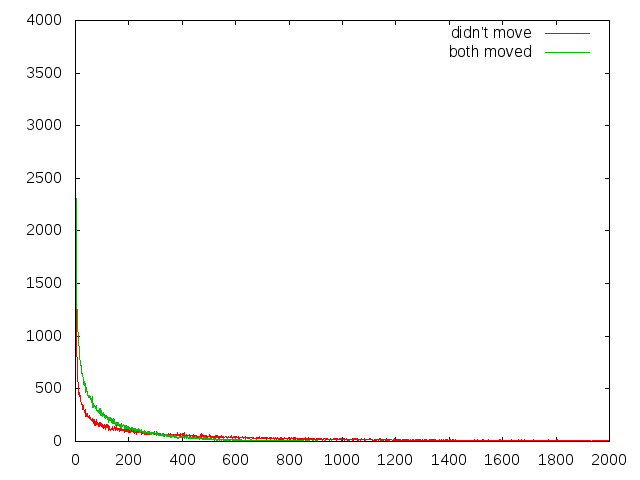
双方動いたときの平均試行回数が131.15286であるのに対し、動かなかったときの平均回数が536.75194。 ちなみに分散はそれぞれ27,592.7712938と692,246.087266。
双方動いたほうが圧倒的に早い!!!!!!!!!!
真面目に考察するなら、「ここにはいなかったからきっとあっちだ」っていう予想をAIがするようになれば、移動しないほうが探索回数の上限が決まるので早いと思う。
無限の大きさを持つホームセンターならどうなるんだろう。